Large-Scale ML [lecture 1\2]
lecture 1
-
标准机器学习过程
- 数据收集和准备:数据收集、数据清洗和预处理(处理缺失值、去除噪声、处理异常值;归一化、特征提取等)
- 模型选择与训练:根据问题类型选择适当的模型类型(如线性回归、决策树、神经网络等)
- validation
- test
- deployment
1
2Q:validation和test的区别?
A:验证阶段主要用于模型的调优,包括选择最佳的超参数和避免过拟合。测试阶段主要用于评估模型的最终性能,衡量模型在未见过的数据上的泛化能力。 -
扩展到大数据上的难点
-
实时数据
1
2Q:具体指什么?ss
A:实时数据是指一些应用场景下的数据,数据持续到来,意味着数据集是变化的。比如物联网的感知场景、视频/广告点击率预测场景、天气预测场景。 -
模型选择,更大范围的参数调整
-
大型数据集上的训练时间
-
对延迟、吞吐量和内存使用有要求的情况下,模型怎么推理和部署
-
-
在扩展机器学习时,应该遵守的原则
使用三个方向的技术:统计学、最优化、系统架构?
-
统计学:通过处理小型随机子样本,可以更轻松地处理大型数据集。
1
具体指什么?
-
最优化:将您的学习任务编写为优化问题,并通过迭代更新模型的快速算法来解决它。
-
并行系统与计算机架构:硬件与算法需要相互匹配。
为扩大规模利用并行和分布式系统形式的额外计算,机器学习计算特别适合专用硬件,例如 GPU
1
2Q:摩尔定理的具体内容?为什么说摩尔定律将不再适用?
A:我们不能再指望通过等待两年让 CPU 速度提高两倍来提高性能和可扩展性
-
-
课程目标
- 通过二次采样快速估计数据统计量
- 通过随机梯度下降 (SGD) 进行快速、可扩展的学习
- 用于改进SGD 的优化技术。小批量、动量、自适应学习率。
- 深度学习框架和自动微分。
- 模型选择和超参数优化。
- 并行和分布式培训。
- 量化、模型压缩和其他快速推理方法。
lecture 2
Estimating the empirical risk with samples:机器学习中的大多数错误或准确度都可以通过经验风险来捕获。
-
经验风险

1
2
3
4Q:函数L怎么理解?
A:输入表示一个笛卡尔积,如果Y是一个集合,则Y×Y表示从Y中选取的两个元素组成的所有可能的有序对。也即,Y×Y是一个包含所有(y1,y2)形式的有序对的集合,其中y1和y2都是Y的元素。所以,该函数接受一个来自Y×Y集合的有序对作为输入,并输出一个实数。在二分类问题中,L为0-1损失函数;线性回归问题中,L可能是均方误差损失函数MSE。
Q:经验风险函数跟L的关系?
A:从上图公式看,L计算单个样本的损失,R计算所有样本损失的平均值。 -
如何对经验风险的计算进行扩展
-
与计算开销相关的因素
- 样本总数n,成本与n成正比:通常经验风险计算不会占用额外的空间,因为只是计算一个标量(损失的平均值),但在某些情况下,可能需要存储中间结果或梯度信息。
- 损失函数L的计算成本:损失函数的复杂度也会影响计算经验风险的效率。简单的损失函数(如均方误差)计算速度较快,而复杂的损失函数(如对比损失或自定义损失函数)可能需要更多的计算资源。
- 评估预测器h的成本:模型的复杂度也会影响计算经验风险的效率。复杂模型(如深度神经网络)通常需要更多的计算资源来计算每个样本的预测结果。
-
措施
-
通过并行化来提高计算效率
数据并行化:数据集划分,在多个计算节点上并行计算每个块的损失,最后合并结果
模型并行化:模型的不同部分在不同的计算资源上并行计算
-
小批量提速下降:每次只计算一个小批量数据的损失
-
硬件加速:利用 GPU 或 TPU 等硬件加速器来并行计算
-
近似计算:使用subsampling来近似计算经验风险,具体见第3点。
-
-
-
近似计算经验风险
- 引入随机变量 Z。这个随机变量 Z 代表从经验风险的求和公式中随机采样一个元素的损失值。

- 多次独立地抽取 Z 的样本,这些样本的平均值将近似于经验风险 R~emp~
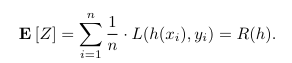
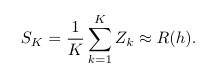

1
2Q:E[Z]是什么意思?
A:表示Z的数学期望。数学期望的定义回顾在上图中。-
近似计算的开销与样本总数n有关系吗?
根据统计学原理,一组独立随机变量的平均值往往聚集在该随机变量的期望值周围,可以形式化地表述为(强大数定律):
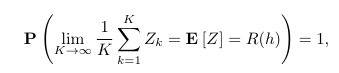
1
2Q:大数定律?
A:描述相当多次数重复实验的结果的定律。根据这个定律知道,样本数量越多,则其算术平均值就有越高的概率接近期望。大数定律主要有两种表现形式:弱大数定律和强大数定律。定律的两种形式都肯定无疑地表明,样本均值收敛于真值。具体在下图。
-
平均值的分布:中心极限定理,当我们有一组独立同分布的随机变量且这些随机变量具有有限的均值和方差时,当抽样次数足够大时,这些随机变量的标准化和中心化的和将近似服从正态分布。N(0,Var(Z))是一个正态分布,其平均值μ=0,方差为Var(Z)。换句话说,随着我们采样更多的 Z,样本平均值会越来越接近真实的期望值 E[Z],且这种接近的误差按照正态分布分布,其方差随着 K 增加而减小。

1
2Q:这个式子怎么形象理解?
A:如下图(标准化后的经验风险误差的分布情况)。横轴表示标准化后的经验风险的误差值,即上图左边的式子,这是抽样平均值与真实期望值之间的差距,经过标准化处理后的值。纵轴表示概率密度,这个值表示在某个误差值附近的概率密度,反映了误差值出现在该范围内的可能性。综上所述,根据中心极限定理,当样本数量足够大时,标准化后的经验风险误差值将趋于图中的正态分布。正态分布的均值为 0,意味着在大量抽样的情况下,经验风险的近似值会围绕真实期望值波动,且平均误差为 0。正态分布的标准差由Var(Z)决定,表示误差的分散程度。标准差越大,分布越宽,意味着误差波动越大;标准差越小,分布越窄,误差波动越小。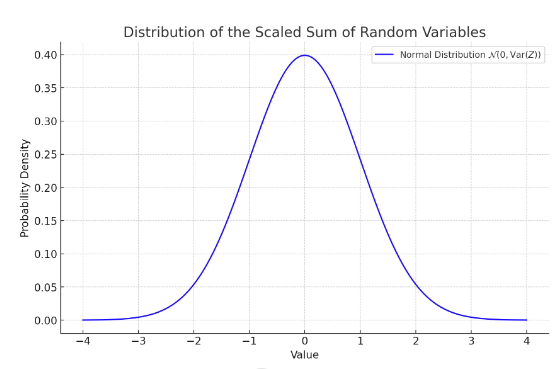
-
需要多长时间才能得到合适的近似值?
1
Q:不太理解,这里概率不等式的意义是什么?为了证明近似计算的正确性,还是为了应用?
浓度不等式:能够限制一个有限总和偏离其期望值的概率。
马尔可夫不等式:如果S是一个非负的随机变量,且具有有限的期望值,则对于任意a>0都有
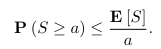
切比雪夫不等式:如果S是一个非负的随机变量,且具有有限的期望值,则对于任意a>0都有
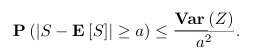
霍夫丁不等式:切比雪夫不等式的一个问题,给出的概率并不够小。虽然我们知道这些总和逐渐接近类似高斯分布的东西,但我们期望从期望值偏离一定程度的概率会随着 a 的增加呈指数级下降,因为这是高斯分布的性质。霍夫丁不等式给出了总和尾部概率的一个更紧密的界限。
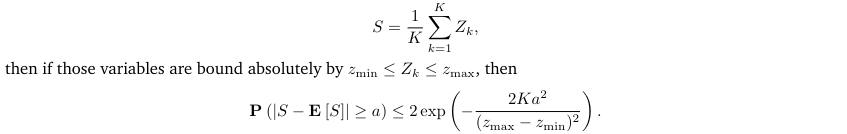
其他不等式
- Azuma’s:对非独立同分布也适用
- Bennett’s:结合了绝对边界和方差的信息,提供了更紧凑的界限。
-
想想?

1
Q:怎么才能得到一个比较好的近似?又需要多少次抽样才能得到这种程度的近似?
