Neural Networks Tutorial

# For tips on running notebooks in Google Colab, see
# https://pytorch.org/tutorials/beginner/colab
%matplotlib inline

Neural Networks

Neural networks can be constructed using the torch.nn package.

Now that you had a glimpse of autograd, nn depends on autograd to define models and differentiate them. An nn.Module contains layers, and a method forward(input) that returns the output.

For example, look at this network that classifies digit images:

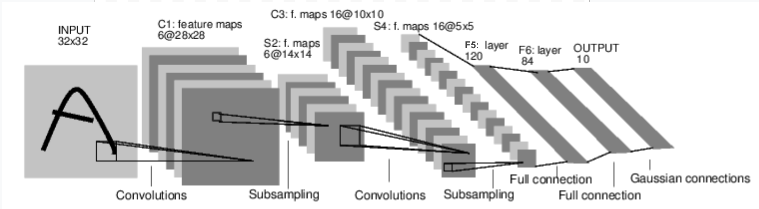
It is a simple feed-forward network. It takes the input, feeds it through several layers one after the other, and then finally gives the output.

A typical training procedure for a neural network is as follows:

• Define the neural network that has some learnable parameters (or weights)定义神经网络
• Iterate over a dataset of inputs在输入数据集上迭代
• Process input through the network通过nn处理输入
• Compute the loss (how far is the output from being correct)计算损失
• Propagate gradients back into the network’s parameters梯度反向传播
• Update the weights of the network, typically using a simple update rule: weight = weight - learning_rate * gradient更新网络参数

Define the network

Let’s define this network:

import torch
import torch.nn as nn
import torch.nn.functional as F


class Net(nn.Module):

    def __init__(self):
        super(Net, self).__init__()
        # 1 input image channel, 6 output channels, 5x5 square convolution；1 个输入图像通道，6 个输出通道，5x5 方形卷积
        # kernel
        self.conv1 = nn.Conv2d(1, 6, 5)# 参数含义依次是：输入的通道数目、输出的通道数目、卷积核的大小（当卷积是方形的时候，只需要一个整数边长即可，卷积不是方形，要输入一个元组表示 高和宽）
        self.conv2 = nn.Conv2d(6, 16, 5)
        # an affine operation: y = Wx + b；仿射运算
        self.fc1 = nn.Linear(16 * 5 * 5, 120)  # 5*5 from image dimension 
        self.fc2 = nn.Linear(120, 84)
        self.fc3 = nn.Linear(84, 10)

    def forward(self, input):
        # Convolution layer C1: 1 input image channel, 6 output channels,卷积层C1：1个输入图像通道，6个输出通道，
        # 5x5 square convolution, it uses RELU activation function, and；5x5方形卷积，它使用RELU激活函数，并且
        # outputs a Tensor with size (N, 6, 28, 28), where N is the size of the batch；输出大小为 (N, 6, 28, 28) 的 Tensor，其中 N 是批次的大小
        c1 = F.relu(self.conv1(input))# 卷积1->激活；(N, 6, 28, 28)（在每个输入通道的大小为32x32的情况下）
        # Subsampling layer S2: 2x2 grid, purely functional,
        # this layer does not have any parameter, and outputs a (N, 6, 14, 14) Tensor
        s2 = F.max_pool2d(c1, (2, 2))# 下采样，kernel=2 x 2；(N, 6, 14, 14)
        # Convolution layer C3: 6 input channels, 16 output channels,
        # 5x5 square convolution, it uses RELU activation function, and
        # outputs a (N, 16, 10, 10) Tensor
        c3 = F.relu(self.conv2(s2))# 卷积2->激活；(N, 16, 10, 10)
        # Subsampling layer S4: 2x2 grid, purely functional,
        # this layer does not have any parameter, and outputs a (N, 16, 5, 5) Tensor
        s4 = F.max_pool2d(c3, 2)# 下采样，kernel=2 x 2；(N, 16, 5, 5)
        # Flatten operation: purely functional, outputs a (N, 400) Tensor
        s4 = torch.flatten(s4, 1)# 展平
        # Fully connected layer F5: (N, 400) Tensor input,
        # and outputs a (N, 120) Tensor, it uses RELU activation function
        f5 = F.relu(self.fc1(s4))# 线性层->激活；(N, 120)
        # Fully connected layer F6: (N, 120) Tensor input,
        # and outputs a (N, 84) Tensor, it uses RELU activation function
        f6 = F.relu(self.fc2(f5))# 线性层->激活；(N, 84)
        # Gaussian layer OUTPUT: (N, 84) Tensor input, and
        # outputs a (N, 10) Tensor
        output = self.fc3(f6)# 线性层->激活；(N, 10)
        return output


net = Net()
print(net)

Net(
  (conv1): Conv2d(1, 6, kernel_size=(5, 5), stride=(1, 1))
  (conv2): Conv2d(6, 16, kernel_size=(5, 5), stride=(1, 1))
  (fc1): Linear(in_features=400, out_features=120, bias=True)
  (fc2): Linear(in_features=120, out_features=84, bias=True)
  (fc3): Linear(in_features=84, out_features=10, bias=True)
)

You just have to define the forward function, and the backward function (where gradients are computed) is automatically defined for you using autograd. You can use any of the Tensor operations in the forward function.

只需要定义 forward 函数， backward 会再使用自动微分时自动执行。

The learnable parameters of a model are returned by net.parameters()

net.parameters() 会返回一个模型中所有可训练的参数。

params = list(net.parameters())
print(len(params))
print(params[0].size())  # conv1's .weight：6为输出通道数（有6个不同的卷积核），1为输入通道数，卷积核形状为5x5

10
torch.Size([6, 1, 5, 5])

由于网络中包含两个卷积层和三个线性层，每层有权重和偏置两组参数可训练，因此参数中总共有十组。
Let’s try a random 32x32 input. Note: expected input size of this net (LeNet) is 32x32. To use this net on the MNIST dataset, please resize the images from the dataset to 32x32.

input = torch.randn(1, 1, 32, 32)# batch_size=1，channels=1，w x h=32x32
out = net(input)
print(out)

tensor([[ 0.0659,  0.1170, -0.1006, -0.0936, -0.0479, -0.0695,  0.0936,  0.0952,
         -0.0907, -0.0092]], grad_fn=<AddmmBackward0>)

Zero the gradient buffers of all parameters and backprops with random gradients:

梯度清空，反向传播梯度（设置一个随机的初始梯度值，该梯度的形状大小需要和out相同）

net.zero_grad()
out.backward(torch.randn(1, 10))

在 PyTorch 中，调用 backward() 方法时，通常用于计算张量相对于模型参数的梯度。当使用 out.backward() 时，PyTorch 会计算 out 对于网络中各个参数的梯度。这在处理标量输出（即一个单一值）时非常常见，因为损失函数通常返回一个标量。

然而，当输出 out 是一个张量而非标量时（例如 out 的形状为 [1, 10]），则需要指定一个与 out 形状相同的张量作为 backward() 的输入参数，告诉 PyTorch 每个输出分量的梯度（或者叫“权重”）是多少。这一步相当于手动指定求导的方向。

NOTE:

torch.nn only supports mini-batches. The entire torch.nnpackage only supports inputs that are a mini-batch of samples, and not a single sample.For example, nn.Conv2d will take in a 4D Tensor ofn Samples x n Channels x Height x Width.If you have a single sample, just use input.unsqueeze(0) to add a fake batch dimension.

在 PyTorch 中，torch.nn 模块设计用于处理小批量数据（mini-batches），而不是单个样本。这意味着很多神经网络层（如 nn.Conv2d）期望输入是一个四维张量，其形状为 (batch_size, n_channels, height, width)，其中 batch_size 是样本的数量。因此，即使你只有一个样本，你仍然需要提供一个具有批量维度的输入张量。

input.unsqueeze(0) 的作用是向你的输入张量 input 添加一个新的维度，表示批量大小。这确保了输入符合 torch.nn 模块的预期格式。(如：input = torch.randn(3, 32, 32)，input = input.unsqueeze(0))

Before proceeding further, let’s recap all the classes you’ve seen so far.

Recap: 回顾

• torch.Tensor - A multi-dimensional array with support for autograd operations like backward(). Also holds the gradient w.r.t. the tensor.
• nn.Module - Neural network module. Convenient way of encapsulating parameters, with helpers for moving them to GPU, exporting, loading, etc.
• nn.Parameter - A kind of Tensor, that is automatically registered as a parameter when assigned as an attribute to a Module.
• autograd.Function - Implements forward and backward definitions of an autograd operation. Every Tensor operation creates at least a single Function node that connects to functions that created a Tensor and encodes its history.

At this point, we covered:

• Defining a neural network：定义一个神经网络
• Processing inputs and calling backward：处理输入，发起反馈

Still Left:

• Computing the loss：计算损失
• Updating the weights of the network：更新网络参数

Loss Function

A loss function takes the (output, target) pair of inputs, and computes a value that estimates how far away the output is from the target.

损失函数采用（输出，目标）输入对，并计算一个值来估计输出与目标的距离。

There are several different loss functions under the nn package . A simple loss is: nn.MSELoss which computes the mean-squared error between the output and the target.

nn 包下有几种不同的损失函数。一个简单的损失是：nn.MSELoss，它计算输出和目标之间的均方误差。

For example:

output = net(input)
target = torch.randn(10)  # a dummy target, for example
target = target.view(1, -1)  # make it the same shape as output
criterion = nn.MSELoss()# 设置损失计算标准

loss = criterion(output, target)# 计算
print(loss)

tensor(0.6975, grad_fn=<MseLossBackward0>)

Now, if you follow loss in the backward direction, using its .grad_fn attribute, you will see a graph of computations that looks like this:

现在，如果使用 loss 的 .grad_fn 属性向后跟踪损失，您将看到如下所示的计算图：

.sh}

input -> conv2d -> relu -> maxpool2d -> conv2d -> relu -> maxpool2d
      -> flatten -> linear -> relu -> linear -> relu -> linear
      -> MSELoss
      -> loss

So, when we call loss.backward(), the whole graph is differentiated w.r.t. the neural net parameters, and all Tensors in the graph that have requires_grad=True will have their .grad Tensor accumulated with the gradient.

因此，调用 loss.backward() 时，整个计算图相对于神经网络的参数进行求导（微分）。对于计算图中的所有张量，如果其 requires_grad 属性为 True，这些张量的 .grad 属性将累积其梯度。

For illustration, let us follow a few steps backward:

loss.grad_fn 是一个与 loss 张量相关的函数，表示计算该张量所涉及的最后一个操作（函数）的梯度函数。具体来说，grad_fn 是一个 Function 对象，它记录了创建该张量的操作，从而使得反向传播过程能够计算梯度。

next_functions 是一个包含后续操作的元组列表。loss.grad_fn.next_functions[0][0] 指向 MseLossBackward 的第一个输入，即 output 的 grad_fn。next_functions[0]是 MseLossBackward 的第一个输入，继续索引到[0]即其grad_fn成员。

print(loss.grad_fn)  # MSELoss（生成loss的操作）
print(loss.grad_fn.next_functions[0][0])  # Linear（生成MSELoss的操作，即MSELoss之前的操作，应该是网络最后一层）
print(loss.grad_fn.next_functions[0][0].next_functions[0][0])  # ReLU（生成Linear的操作，即Linear之前的操作，应该是激活函数）

<MseLossBackward0 object at 0x00000175696E4BB0>
<AddmmBackward0 object at 0x00000175696E48B0>
<AccumulateGrad object at 0x00000175696E4BB0>

Backprop

To backpropagate the error all we have to do is to loss.backward(). You need to clear the existing gradients though, else gradients will be accumulated to existing gradients.

为了反向传播误差，我们所要做的就是loss.backward()。但是需要先清除现有的梯度。

Now we shall call loss.backward(), and have a look at conv1’s bias gradients before and after the backward.

net.zero_grad()     # zeroes the gradient buffers of all parameters

print('conv1.bias.grad before backward')
print(net.conv1.bias.grad)

loss.backward()

print('conv1.bias.grad after backward')
print(net.conv1.bias.grad)

conv1.bias.grad before backward
None
conv1.bias.grad after backward
tensor([-0.0133,  0.0036,  0.0017,  0.0051,  0.0013, -0.0003])

Now, we have seen how to use loss functions.

Read Later:

The neural network package contains various modules and loss functions that form the building blocks of deep neural networks. A full list with documentation is here.

The only thing left to learn is:

• Updating the weights of the network

Update the weights

The simplest update rule used in practice is the Stochastic Gradient Descent (SGD):

.python}

weight = weight - learning_rate * gradient

We can implement this using simple Python code:

.python}

learning_rate = 0.01
for f in net.parameters():
    f.data.sub_(f.grad.data * learning_rate)

However, as you use neural networks, you want to use various different update rules such as SGD, Nesterov-SGD, Adam, RMSProp, etc. To enable this, we built a small package: torch.optim that implements all these methods. Using it is very simple:

torch.optim 来实现参数更新

.python}

import torch.optim as optim

# create your optimizer
optimizer = optim.SGD(net.parameters(), lr=0.01)

# in your training loop:
optimizer.zero_grad()   # zero the gradient buffers梯度清空
output = net(input)
loss = criterion(output, target)
loss.backward()
optimizer.step()    # Does the update

NOTE:

Observe how gradient buffers had to be manually set to zero usingoptimizer.zero_grad(). This is because gradients are accumulatedas explained in the Backprop section.

optimizer.zero_grad() 和 net.zero_grad() 都可以用来清零模型参数的梯度，但它们的用法和场景有所不同。

1. optimizer.zero_grad()

• 适用场景：一般情况下，尤其是当你使用优化器（如 torch.optim.SGD、torch.optim.Adam 等）来更新模型参数时，通常会使用 optimizer.zero_grad() 来清零梯度。

• 原因：优化器（optimizer）管理着你传给它的模型参数（params），当你调用 optimizer.zero_grad() 时，实际上它会遍历所有的参数，并清除这些参数上的梯度。因此，当你使用 optimizer.step() 来更新参数时，确保梯度累积是从零开始的。

• 推荐使用：大多数情况下，如果你使用优化器来更新参数，应该使用 optimizer.zero_grad()。

2. net.zero_grad()

• 适用场景：net.zero_grad() 通常用于你手动管理模型参数的情况，或者你希望直接控制模型中的所有参数的梯度，而不通过优化器。比如当你没有创建优化器，或在一些自定义的优化过程时。

• 原因：net 是一个 nn.Module，它的 zero_grad() 方法会递归遍历这个网络中的所有模块，并将所有参数的梯度清零。因此，net.zero_grad() 是清除整个模型的梯度的另一种方式。

• 使用场景：这种方法在你想要清除特定模型的梯度，或者不使用标准的优化器进行训练时可能会用到。

关键区别

• optimizer.zero_grad()：清除由优化器管理的参数的梯度。它适合常规的训练过程，尤其是在多模型或多个优化器的情况下，使用 optimizer.zero_grad() 是更好的选择，因为它只清除相关参数的梯度。

• net.zero_grad()：清除整个模型（net）中所有参数的梯度。它适合一些特殊情况，例如你手动更新参数，或者你不使用标准的优化器进行训练。

例子

通常，代码中会这样写：

optimizer.zero_grad()   # 清零梯度
output = net(input)     # 前向传播
loss = criterion(output, target)  # 计算损失
loss.backward()         # 反向传播计算梯度
optimizer.step()        # 更新参数

这种情况下，optimizer.zero_grad() 会清除由 optimizer 管理的参数的梯度。

如果你没有使用优化器，而是手动更新参数：

net.zero_grad()         # 清零梯度
output = net(input)     # 前向传播
loss = criterion(output, target)  # 计算损失
loss.backward()         # 反向传播计算梯度

# 手动更新参数
with torch.no_grad():
    for param in net.parameters():
        param -= learning_rate * param.grad

在这种情况下，使用 net.zero_grad() 清除整个模型的梯度。

总结

• 使用 optimizer.zero_grad() 是常见的做法，因为它只清除优化器管理的参数梯度。
• net.zero_grad() 是一种更广泛的方式，清除整个模型的梯度，适用于手动管理参数或不使用优化器的情况。