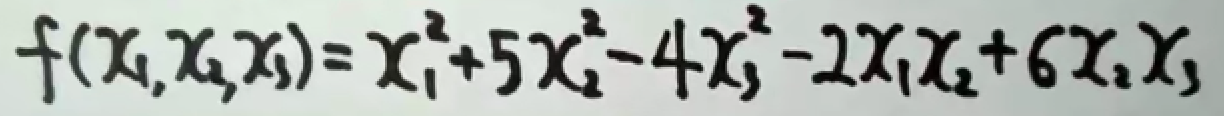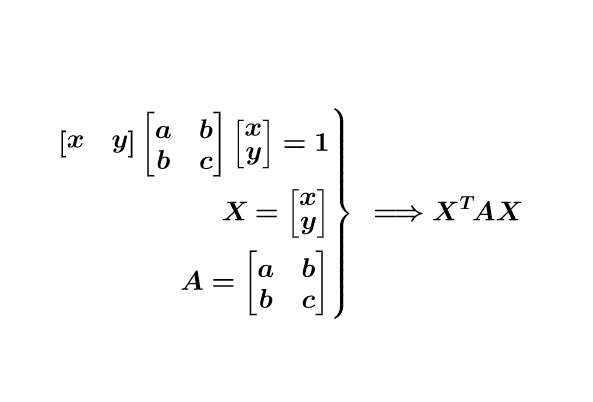计算非线性函数的 Hessian 矩阵

现有函数 $f(w)=w_1^2+2w_2^2+3w_3^2$ ，其中 $w=[w_1,w_2,w_3]^T$ 。

计算一阶导数（梯度）

首先对每个变量 $w_i$ 求一阶偏导数：
$\frac{\partial f}{\partial w_1}=2w_1 \\ \frac{\partial f}{\partial w_2}=4w_2 \\ \frac{\partial f}{\partial w_3}=6w_3$
因此，梯度向量 $\nabla f(w) = (w2_1,4w_2,6w_3)^T$ 。
计算二阶导数： Hessian 矩阵

矩阵元素 $H_{ij}$ 是 $f$ 对 $w_i$ 和 $w_j$ 的二阶偏导数：
$H_{ji} = \frac{\partial^2 f}{\partial w_i \partial w_j}$
逐个计算得到下面的结果，其他二阶偏导数都为 $0$ 。
$\frac{\partial^2 f}{\partial w_1^2} = 2 \\ \frac{\partial^2 f}{\partial w_2^2} = 4 \\ \frac{\partial^2 f}{\partial w_3^2} = 6$
因此， Hessian 矩阵如下：
$\left[\begin{array}{ccc} 2 & 0 & 0 \\ 0 & 4 & 0 \\ 0 & 0 & 6 \end{array}\right]$

特征值的求法

矩阵特征值和特征向量定义

$A$ 为 $n$ 阶矩阵，若有常数 $\lambda$ 和 $n$ 维非 $0$ 列向量 $x$ 满足 $Ax = \lambda x$ ，则称 $\lambda$ 为 $A$ 的特征值， $x$ 为 $A$ 对应于特征值 $\lambda$ 的特征向量。

$Ax = \lambda x$ 可写作 $(A - \lambda E)x = 0$ ，且 $|A - \lambda E|$ 为 $A$ 的特征多项式，称 $|A - \lambda E| = 0$ 为 $A$ 的特征方程。特征方程是一个齐次线性方程组，求解特征值的过程就是求解特征方程的解的过程。

三阶矩阵特征值的快速求法

不妨令：

A= \left[\begin{array}{ccc} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{array}\right]

其特征多项式为：

|\lambda E - A| = \left|\begin{array}{ccc} \lambda - a_{11} & -a_{12} & -a_{13} \\ -a_{21} & \lambda - a_{22} & -a_{23} \\ -a_{31} & -a_{32} & \lambda - a_{33} \end{array}\right|

直接展开得到：

|\lambda E - A| = \lambda ^3 - (a_{11}+a_{22}+a_{33}) \lambda^2 + k\lambda - |A|

即：

|\lambda E - A| = \lambda ^3 - tr(A) \cdot \lambda^2 + k\lambda - |A|

此处 $k$ （主对角线元素错乘 - 对称位置元素相乘）：

k = (a_{11}a_{22}+a_{11}a_{33}+a_{22}a_{33}) - (a_{12}a_{21}+a_{13}a_{31}+a_{23}a_{32})

特征值的意义

从 $Ax = \lambda x$ 来看， $Ax$ 表示对向量 $x$ 进行一次线性变换（旋转或拉伸），而该转换的效果为 $\lambda x$ ，即只进行拉伸。

求解特征值和特征向量，可以看作求出矩阵能使哪些向量只发生拉伸、拉伸的程度如何（特征值大小）。这样做的意义在于，看一个矩阵在哪些方面能产生最大的效果，并根据所产生的每个特征向量（一般研究特征值最大的那几个）进行分类讨论与研究。

几何意义

谱范数

对于任意两点间来说，直线距离最短。而计算两点间距离的公式就是源于众所周知的勾股定理的基础上推导而来的。事实上，不仅对于人们所熟知的二维空间和三维空间如此，对于高维空间亦是如此。在数学上，一般将高维空间的点表示为一个多维向量，而任意一个点到原点的直线距离则称为该点的二范数。

下面主要讨论一种拓展版的二范数，即矩阵的二范数。不过，人们一般称之为矩阵的谱范数。在科研中，该范数也有着极为广泛的应用，例如度量一个矩阵的大小，判断算法是否收敛等。

对于实矩阵 $A$ ，其谱范数定义如下：

\rho = \sqrt{max_{\lambda_i}(eig(A^T \times A))}

其中 $eig(A)$ 表示计算方阵 $A$ 特征值，返回向量 $[\lambda_1,\lambda_2,\dots,\lambda_n]^T$ ，其中 $\lambda_i$ 表示第 $i$ 个特征值。向量的二范数表示一个空间点到原点的距离/向量长度，矩阵的谱范数表示什么？

意义

如果将矩阵看作一种对于向量的变换方式（拉伸、转向、映射等），则矩阵谱范数的物理意义是对于任意一个向量，在矩阵变换后，新向量的长度小于等于原来向量的长度乘以该矩阵的谱范数，即：

||x^`||_2 \leq \rho \cdot ||x||_2

换句话说，任何一个向量经过该矩阵变换后，其长度变化是有限的。

二次型

参考：

https://szup.github.io/2021/03/04/0303-square-form/

定义

$n$ 个变量的二次多项式称为二次型，即在一个多项式中，未知数的个数为任意多个，但每一项的次数都为 $2$ 的多项式。

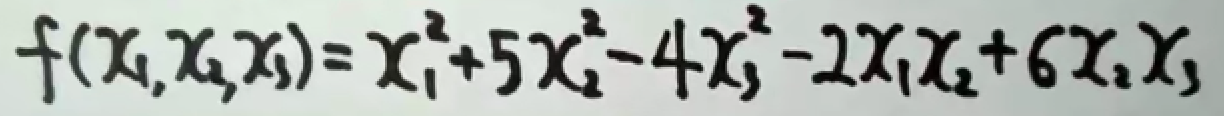
二次型的矩阵表示

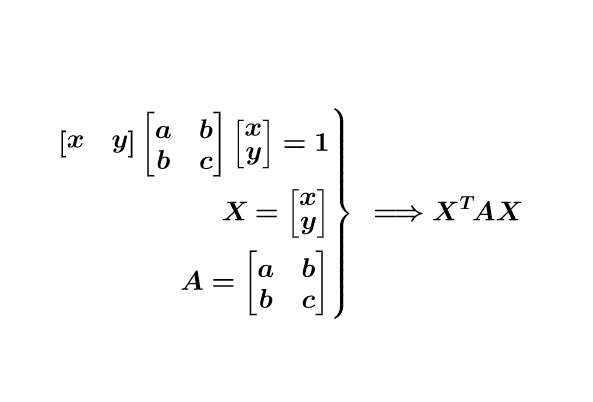
秩

对称矩阵A的秩就是二次型的秩。

Review of Linear Algebra