激活函数

线性激活函数的局限性：线性变换具有可合并性，即两个线性变换的复合仍然是一个线性变换，其实整个网络跟单层神经网络是等价的。

非线性激活函数（ReLU、Sigmoid等）的必要性：每一层输出经过非线性变换，打破了线性变换的可合并性，从而使网络能够表示更加复杂的非线性函数关系。

激活函数性质

  1. 非线性

  2. 可微性：当优化方法是基于梯度的时候，就体现了该性质

  3. 单调性： 当激活函数单调时，单层网络能够保证是凸函数

  4. f(x)≈x： 当激活函数满足这个性质的时候，如果参数的初始化是随机的较小值，那么神经网络的训练将会很高效；否则需要谨慎设置初始值

  5. 值域

    • 值域受限

      • 梯度也会相对稳定，梯度更新较小，避免了训练过程中出现剧烈的参数变化，从而提升了训练的稳定性。
      • 由于输出值的范围有限，特征表示会受到限制。这意味着每个神经元的输出不会有非常大的差异，权值的变化对输出的影响更加显著。

    • 值域不受限

      • 输出值无限时，梯度可以变得非常大，模型的训练可能更加高效，因为大的梯度更新会导致权值变化更快，从而加速收敛。
      • 但是输出值无限的激活函数在训练过程中容易导致梯度爆炸，尤其是在深层网络中。因此学习率需要设置一个较小的数以保证训练的稳定性。
      1
      2
      Q：梯度爆炸？
      A：梯度爆炸是指在神经网络训练过程中，梯度的值在反向传播中变得非常大，导致参数更新过大，从而使得模型参数不稳定，训练过程无法有效进行。我们可以通过图形来理解这一现象。蓝线表示稳定的训练过程，梯度值随着训练迭代线性增加，保持在一个可控范围内。红线表示不稳定的训练过程，梯度值随着训练迭代指数级增加，变得非常大。梯度爆炸的原因：1）在非常深的网络中，梯度在多层反向传播时会不断相乘。如果某些层的梯度值很大，经过多层传递后会导致梯度指数级增长。2）权重初始化值过大，也会导致梯度在前向传播和反向传播过程中不断放大。3）学习率设置过大，每次参数更新的步伐过大，容易引发梯度爆炸。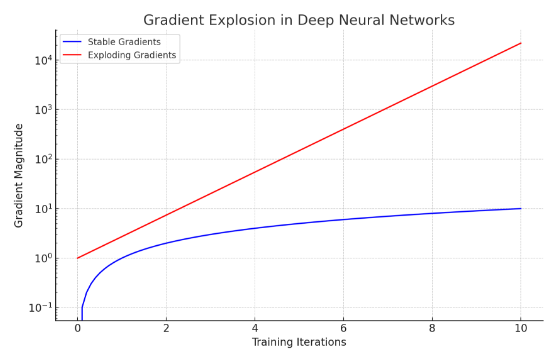

      image-20240612151538330

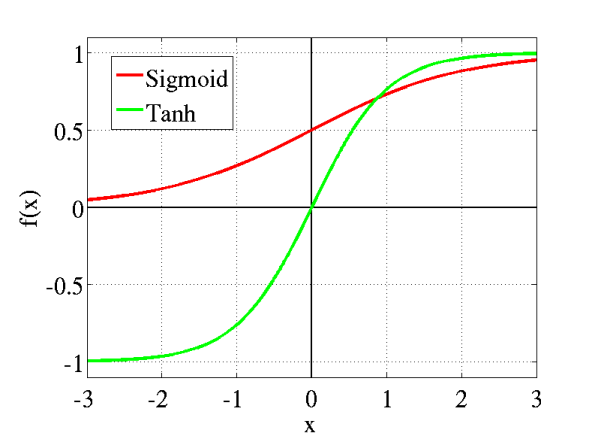
传统Sigmoid系激活函数

从数学上来看，非线性的Sigmoid函数对中央区的信号增益较大，对两侧区的信号增益小，在信号的特征空间映射上，有很好的效果。

img

1
2
3
4
5
6
7
8
9
10
# torch中的三种用法
input = torch.tensor([1, 2, 3])

# 1.
torch.sigmoid(input)
# 2.
torch.nn.functional.sigmoid(input)
# 3.注意这里的用法
mod = torch.nn.Sigmoid()
mod(input)

近似生物神经激活函数ReLU

两种方式
1
2
3
4
5
6
# 1.
import torch.nn.functional as F
out = F.relu(input)
# 2.
import torch.nn as nn
nn.ReLU()

使用场景不同

  • F.relu()是函数调用，一般使用在foreward函数里
  • nn.ReLU()是模块调用，一般在定义网络层的时候使用
原理

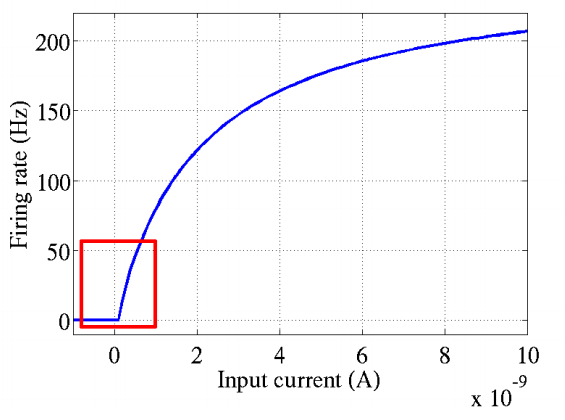
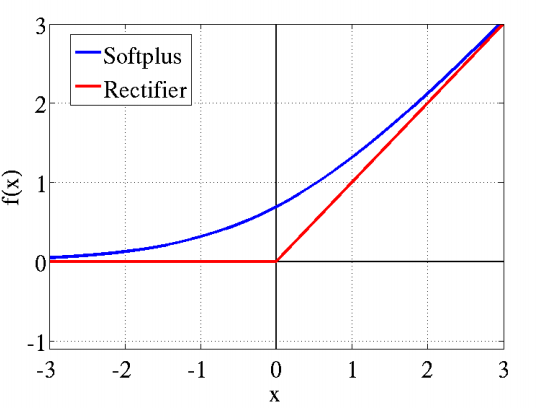
脑神经元接受信号更精确的激活模型模拟图如下，可以看到红框里前端状态完全没有激活。Softplus&ReLU都类似其形状。详情见Deep Sparse Rectifier Neural Networks。

img

img