FIGRET: Fine-Grained Robustness-Enhanced Traffic Engineering

Ximeng Liu, Shizhen zhao, Yong Cui, and Xinbing Wang. 2024. FIGRET: Fine-Grained Robustness-Enhanced Traffic Engineering. In ACM SIGCOMM 2024 Conference (ACM SIGCOMM ’24), August 4–8, 2024, Sydney, NSW, Australia. ACM, New York, NY, USA, 19 pages. https://doi.org/10.1145/3651890.3672258

名词/概念

average Maximum Link Utilization

平均最大链路利用率是指在网络性能分析中，针对所有网络链路计算它们的最大利用率，然后对这些最大值进行平均。解释如下：
- Maximum Link Utilization：单个链路的最大利用率，指该链路在某段时间内承载流量的最高峰值，占其最大带宽的百分比。
- Average of Maximum Link Utilization：对所有链路的最大利用率求平均值，目的是衡量整个网络中链路利用的高峰状态，提供对网络性能的总体概览。
MLU表示网络中某些链路在流量高峰期的负载情况。过高的MLU意味着某些链路在高峰时段几乎接近其最大带宽，可能会导致拥塞、丢包和更高的延迟，从而影响网络的稳定性和用户体验。

流量工程的目标是在尽可能平衡网络负载的情况下有效利用所有链路，减少某些链路的过载。降低MLU意味着网络中的高峰流量能够更均匀地分布在所有链路上，减少某些链路的拥堵风险，从而提升网络的性能和可靠性。

因此，MLU的降低通常是网络优化的一项重要指标，它表明网络中高负载链路的负担减轻，网络能够更加均衡地处理流量负载，从而提高了整体的效率和稳定性。
Traffic Engineering (TE)

流量工程通常通过软件定义网络（SDN）中的集中式控制器来实现。该控制器定期解决网络优化问题，以便高效地分配和路由网络流量。具体步骤如下：
- 优化问题求解：控制器会周期性地根据当前网络状态、流量需求等信息，计算出最优的网络路径分配方案。目的是最大化资源利用率、降低延迟、减少拥塞等。
- 路由器配置下发：一旦得到最优解，控制器会将这些方案转化为实际的路由器配置，确保网络设备能够按照优化后的方案执行流量转发。
Software-Defined Networking (SDN)

软件定义网络，是一种网络管理方法，通过将网络控制层与数据转发层分离，提供更灵活和集中化的控制。
- 控制与数据分离：
  - 传统网络设备（如路由器和交换机）同时负责控制（决定流量路径）和数据转发（实际转发流量）。
  - SDN将这两者分离，控制层由一个集中式控制器（通常是软件）管理，而数据层仅负责根据控制器的指令执行数据包的转发。
- 集中控制：
  - 在SDN中，网络的控制功能集中在一个或多个控制器上。这个集中式控制器具有全局的网络视图，能够根据实时网络状态和流量需求做出智能决策，并将这些决策下发给网络设备。
- 可编程性：
  - SDN的控制器可以通过软件进行编程和动态配置，使得网络管理更加灵活，可以快速调整网络配置，以适应流量变化或实现特定的性能目标。
- 开放接口：
  - SDN通常使用开放的通信接口（如OpenFlow协议）来实现控制器与网络设备之间的通信。这使得不同厂商的设备可以互操作，提升了网络的灵活性和可扩展性。
GEANT WAN

GEANT是一个覆盖欧洲的学术和研究网络，属于广域网（WAN）的一部分，提供高带宽和低延迟的连接。主要用于连接不同的研究机构和大学，支持科研数据的传输和共享。

GEANT的拓扑结构通常涉及多个核心路由器和交换机，形成一个复杂的网络，不局限于特定的机架结构。
PoD（Point of Delivery Level）

PoD代表“交付点”，通常指的是数据中心中网络的一个层级或区域，包含多个**Top of Rack (ToR)**交换机。

在PoD级别，多个机架（rack）被连接到同一个PoD交换机，通常有多个PoD交换机以实现冗余和负载均衡。

这种架构使得数据中心内部的流量能够高效地在不同的机架之间路由。

GEANT WAN和PoD/ToR交换节点都可以配置为监控和捕获经过的流量数据。这些交换节点记录数据包的转发需求，包括流量来源、目标、带宽使用情况等信息。

在捕获和分析流量数据后，可以计算每个交换节点（无论是GEANT中的核心交换节点，还是PoD/ToR中的局部交换节点）的最大链路利用率。
直连拓扑网络

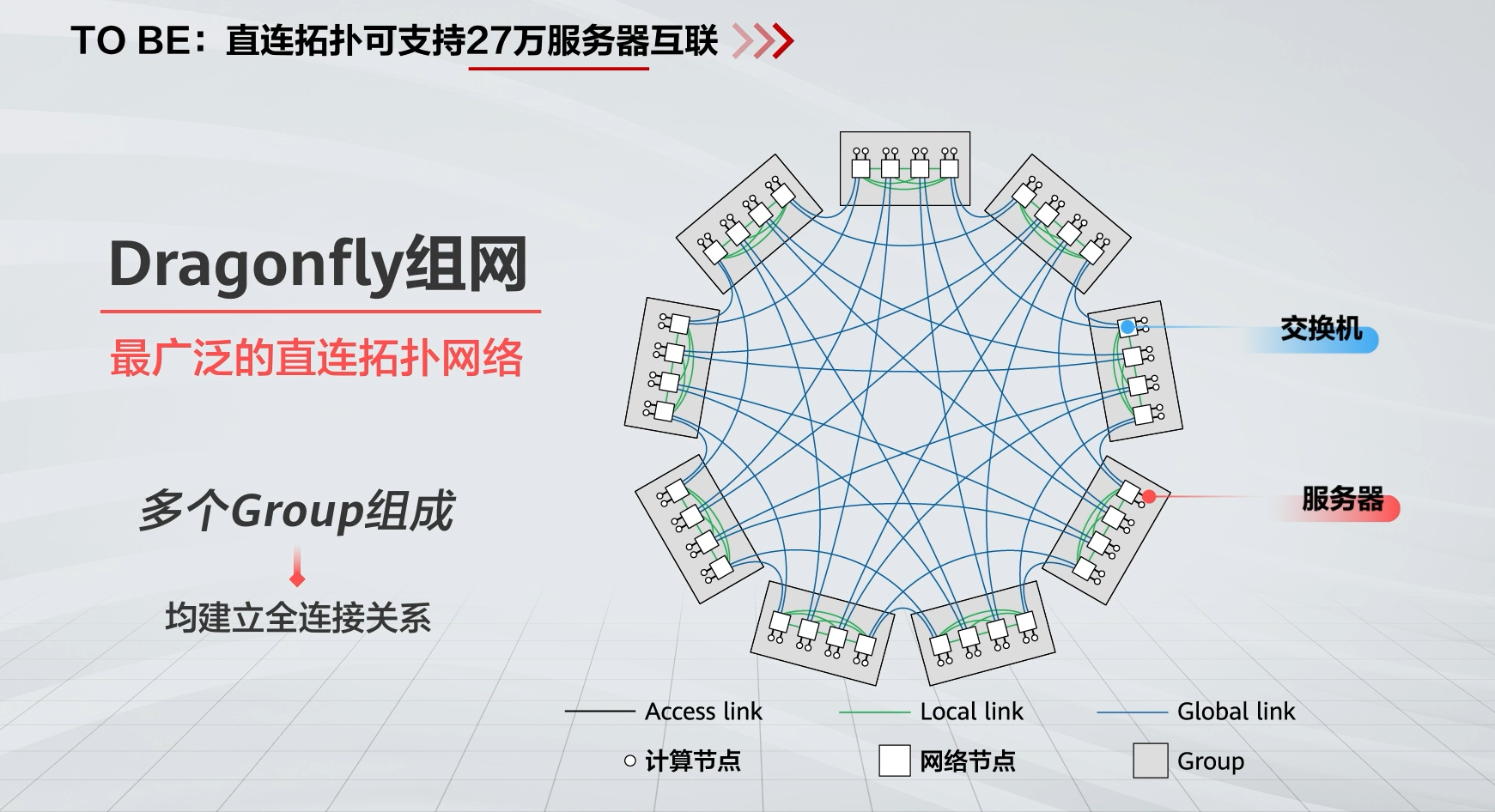
每个网络节点都与计算节点直接相连，不存在专门用于网络节点间互连的网络设备。

注意，组内的网络节点是全连接，组与组之间也是全连接。

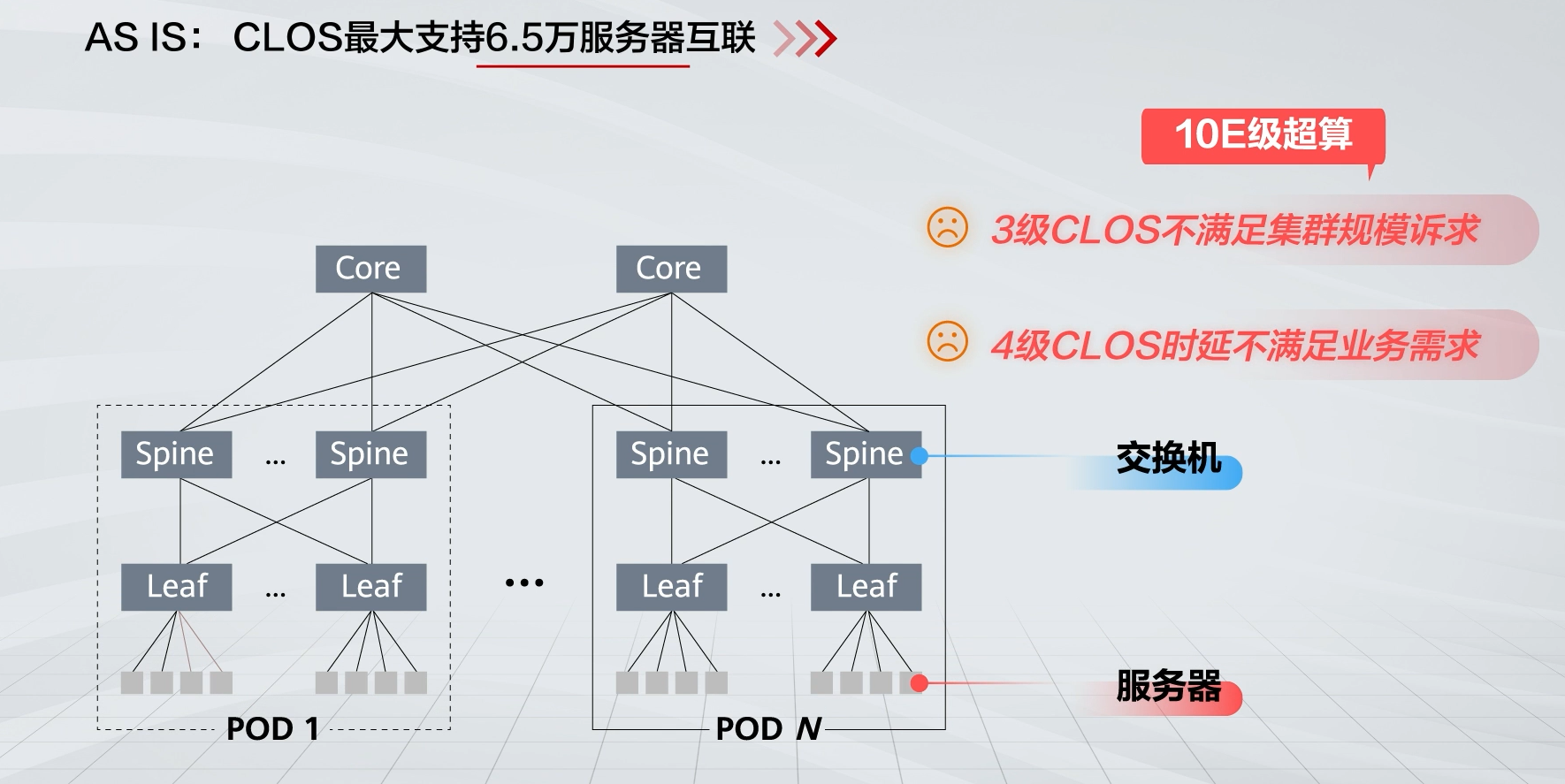
与Clos网络对比：由于3级Clos不满足集群规模需要，4级时延又不满足业务需求，直连拓扑网络支持接入更大规模的终端节点，且网络直径小、网络时延低
Traffic demand与Traffic volumn
- Traffic Demand（流量需求）：
  - 指的是在特定时间内，从源到目的地所需的流量。这通常是对网络中流量需求的预测，反映了用户或应用程序对带宽的需求。
- Traffic Volumes（流量）：
  - 指的是实际传输的数据量，通常以比特、字节或包为单位来度量。是流量需求的实际表现，显示了在给定时间段内网络中传输的流量。
Flow-Completion time(FCT)

一个流（从源节点到目标节点的数据包集合）从开始发送到完全接受所需要的时间。

研究背景

随着网络流量的指数级增长，数据中心网络和广域网（WAN）越来越依赖于**流量工程（TE）来优化网络性能。流量工程通常通过软件定义网络（SDN）**中的集中式控制器实现，它定期解决网络流量的优化问题，以高效地在网络路径上分配流量，并将这些优化结果转化为路由器配置。

问题

流量工程面临的主要挑战之一是如何应对突发性流量。由于控制器在收集流量需求、计算新的流量工程解决方案以及更新转发规则时会引入一定的延迟，因此需要在实际流量到来之前，基于历史数据预先计算网络配置。然而，网络流量具有动态性和不可预测性，这使得准确预测流量变得困难。如果无法充分应对突发流量，可能导致网络拥塞，从而引发延迟增加、数据包丢失率上升以及网络吞吐量下降。因此，提升流量工程系统对突发流量的鲁棒性至关重要。

本文方案

FIGRET（Fine-Grained Robustness-Enhanced Traffic Engineering）旨在通过细粒度的定制化鲁棒性增强策略来提升流量工程的性能，其核心思想如下：

定制化的鲁棒性增强：
- FIGRET根据每个源-目的对的流量特性，对不同源-目的对应用不同的鲁棒性要求：
  - 对于流量稳定的源-目的对，施加较为宽松的鲁棒性要求。
  - 对于易发生突发流量的源-目的对，施加更严格的鲁棒性要求。
- 与其他方案类似，FIGRET使用路径敏感性度量来评估突发流量对路径的影响，并通过限制路径敏感性来增强网络的鲁棒性。
- 不同的是，FIGRET根据网络拓扑和源-目的对的流量特性，定制化路径敏感性约束，从而在突发流量和非突发流量之间实现精细化的鲁棒性增强和平衡。
优化计算方法：
- FIGRET的原始公式可以通过线性规划来求解，但存在两个问题：
  1. 流量预测困难：由于某些源-目的对具有高度突发性，难以准确预测流量矩阵。
  2. 计算复杂度高：线性规划在处理大规模网络时计算复杂度较高，难以扩展。
- 为了解决这些问题，FIGRET采用深度神经网络加速流量工程的计算：
  - FIGRET借鉴了DOTE的思路，直接将历史流量模式映射到路由权重配置，从而消除对流量预测的需求。
  - 为了处理路径敏感性约束，FIGRET在其损失函数中加入一个额外项，专门用来捕捉定制化的鲁棒性要求。

实验评估

实验设置

数据集和拓扑：
- 实验使用了公开的广域网（WAN）数据集以及数据中心PoD级和ToR级的拓扑和流量数据。
- 拓扑规模从几十个节点到数百个节点不等，流量数据包括了低、中、高突发性的各种流量特性。
评估目标：
- 评估FIGRET在不同网络拓扑和流量特性下的性能，尤其是其在突发流量环境中的表现。
- 与谷歌生产数据中心的流量工程系统【36】以及DOTE（一种以最大链路利用率优化为目标的深度学习流量工程系统）【35】进行对比。

实验结果

与谷歌生产数据中心的TE系统对比：
- FIGRET在多个拓扑下，实现了**9%-34%的平均最大链路利用率（MLU）**降低。
- 在解决方案速度上，FIGRET的性能提高了35倍至1800倍。
与DOTE的对比：
- 在两个具有突发性流量的拓扑中，FIGRET相较于DOTE在平均MLU上分别减少了4.5%和5.3%。
- FIGRET同时显著减少了由流量突发导致的严重拥塞事件，分别降低了41%和53.9%。
稳定流量拓扑中的表现：
- 在稳定流量的拓扑中，FIGRET的表现至少与DOTE相当，尽管其额外考虑了鲁棒性要求。

精读理解

FIGRET的研究动机&主要见解

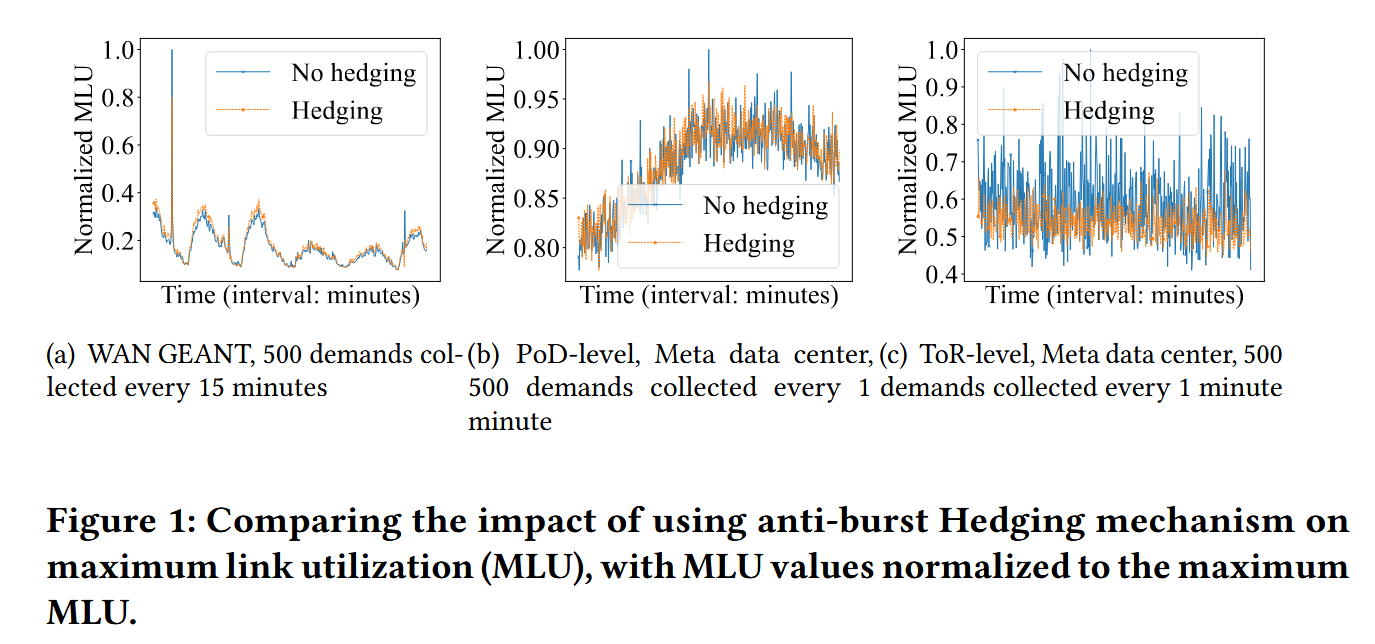
处理突发流量的必要性
- 文章通过分析突发流量对网络性能的影响，强调了在流量工程中管理突发流量的必要性。
  
  在分析中，实施了两种策略进行比较：
  - 无对冲策略（No hedging strategy）：仅使用当前流量矩阵配置下一个时间段，不管理突发流量。
  - 对冲策略（Hedging strategy）：使用当前流量矩阵配置下一个时间段，同时采用对冲机制（将流量分散到多条路径上），防止突发流量对单一路径的影响过大。
- 分析结果
  - 不同网络中突发流量对网络性能的影响：从 GEANT WAN 到PoD级别，再到ToR级别（都是数据中心网络），流量变得更加波动，导致无对冲策略的性能越来越不稳定。
  - 处理突发流量的必要性：
    
    在 GEANT WAN 和数据中心网络中，无对冲策略下，最大链路利用率（MLU）曲线出现更高的峰值，表明网络很可能在没有对冲策略的情况下会因突发流量而拥堵。
    
    无对冲策略下，MLU曲线表现更低的谷值（即流量稳定、无突发大流量的场景下，该策略的网络性能更好），而对冲策略在相同条件下不能达到这样的低谷（因为该策略可能使得大量流量通过非最优路径进行转发）。
- 引出研究动机
  
  管理突发流量在流量工程中是必要的，但这种策略往往会妨碍普通场景下的网络性能。因此，研究的方向是寻找一种能够有效管理突发流量，同时最小化对非突发场景性能影响的流量工程方法。
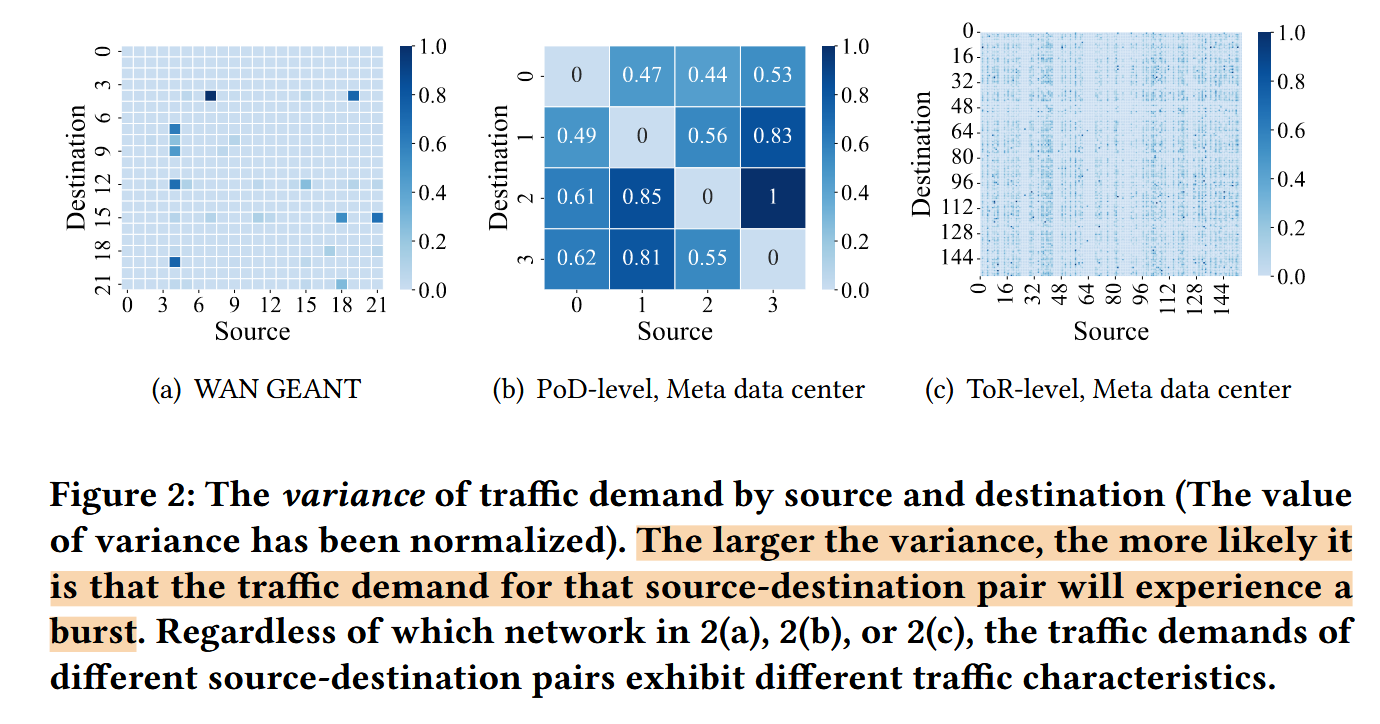
不同源-目的对（简称SD对）下的流量特性不同
- 在GEANT WAN和Meta的数据中心网络（PoD级别和ToR级别）上进行分析，观察不同SD对下流量的特性。
- 分析结果
  
  无论是什么类型的网络，从什么网络级别分析，不同SD对下，流量突发的程度都存在差异。这里利用流量的方差来衡量流量的不稳定性，方差越大，该SD对下越可能出现突发流量。
- 引出研究动机
  - 流量特征差异性：考虑到不同SD对的流量特征不一，将所有SD对的流量视为相同可能导致流量工程（TE）方案的性能不佳。在非突发场景中可能出现次优性能，或在突发情况下牺牲处理能力。
  - 优化TE方法：因此，充分利用这些多样的流量特征在TE中至关重要，以更好地平衡突发流量与非突发流量场景下的网络性能。
不同TE方案下网络性能的表现
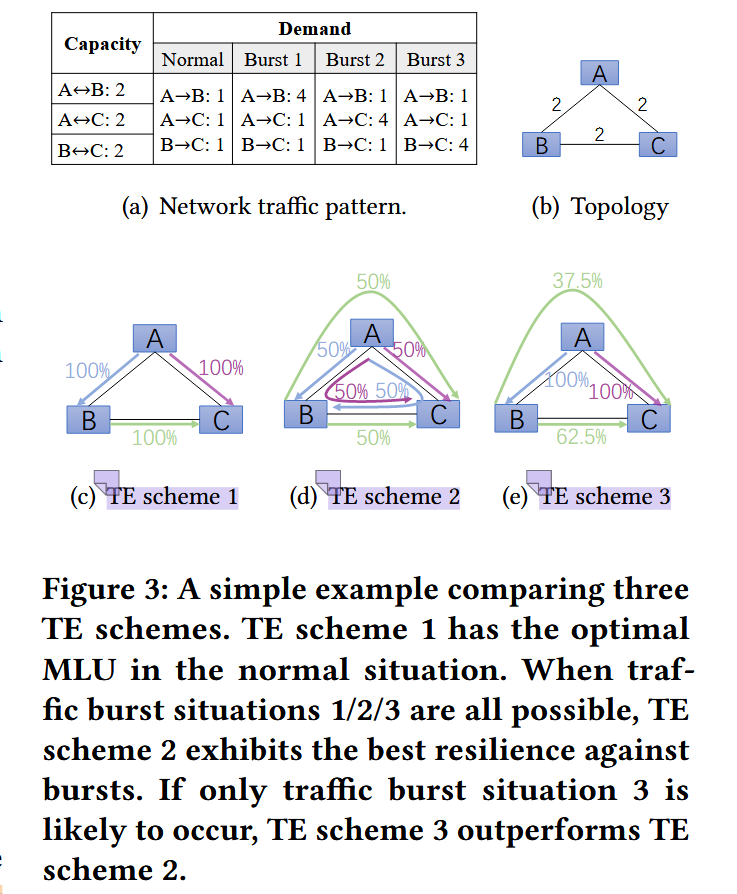
- SCHEME 1
  
  普通场景和突发场景下，都选择最短路径，也即，把需要发送的流量全部通过最短的路径转发，因此图上每条路径写了100%。
  
  这种方案缺少处理突发流量的能力。
- SCHEME 2
  
  普通场景和突发场景下，都进行流量均衡转发，如A到B需要发送1的流量，该方案把0.5通过A->B路径转发，另外0.5通过A->C->B转发，因此图上写50%。
  
  这种方案为了处理突发流量，牺牲了非突发流量场景下的网络性能。
- SCHEME 3
  
  普通场景和突发场景下，专注处理更不稳定的流量需求，如这里的Burst3，方案在任何场景下都将B->C的流量分成两份转发，A->B和A->C都选择最短路径转发。
  
  如果流量需求始终保持稳定，则无需考虑满足该流量需求的路径的稳健性。因此，在Burst3情况和Normal场景下，该方案的表现比方案2更好。也即该方案在正常情况下的性能和突发情况下的性能之间实现了更好的平衡（在普通场景下，方案3的表现没有2的那么差，且又能针对更不稳定的流量进行处理，即实现了一种平衡）。

TE Model

基本定义

Network

使用图表示拓扑网络：

$G = (V,E,c)$
- $V$ ：网络节点的集合。
- $E$ ：网络链路的集合。
- $c$ ：链路容量的映射关系，如 $c(e) = 2$ 表示链路 $e$ 的容量为2。
Traffic demands
- $D$ ：需求矩阵，表示整个网络中的流量转发需求，其形状为 $|V|×|V|$ ， $|V|$ 表示网络节点的数量。
- $D_{ij}$ ：从源节点 $i$ 到目标节点 $j$ 的流量需求。
Network paths
- $p$ ：由TE配置决定的转发路径，如TE决策通过A->B->C这条路径转发源节点A到目标节点C的流量时，A->B->C就是服务于SD对（A，C）的网络路径。
- $P_{sd}$ ：转发路径的集合，服务于源节点 $s$ 到目标节点 $d$ 的流量转发需求。例如源节点 $s$ 到目标节点 $d$ 的流量通过两条路径 $p_1$ 和 $p_2$ 转发，则 $P_{sd} = \{p_1,p_2\}$ 。
Path capacity
- $C_p$ ：网络路径 $p$ 的容量，取决于沿途各边中最小的链路容量。

TE问题

配置
- $\mathcal{R}$ ：一个TE配置。对于每个SD对，该配置指明了将 $D_{sd}$ 规定的流量应该怎样分散到 $P_{sd}$ 中的路径进行流量转发（如每条路径均等地转发流量）。
- $r_p$ ：由TE配置规定，表示沿路径 $p$ 转发的源节点 $s$ 到目标节点 $d$ 的流量需求分数。 $P_{sd}$ 中所有路径的流量需求分数之和应该为1，即满足下式的条件。
  $\sum_{p \in P_{sd}} r_p = 1$
目标：最小化最大链路利用率（the Max Link Utilization, MLU）

Q：为什么最小化最大链路利用率能改善网络性能？

A：Google发现，MLU可以作为吞吐量的代理指标，也能衡量TE方案对网络中流量模式变化的适应/调节能力。高MLU值说明网络中有多条链路过载，而链路过载会导致丢包、吞吐量降低和FCT的增加。
- $f_e$ ：给定网络拓扑 $G$ 、流量需求矩阵 $D$ 和TE配置 $\mathcal{R}$ 的情况下，经过链路 $e$ 的总流量，该值满足下面的式子：
  $f_e = \sum_{s,d \in V, p \in P_{sd},e \in p} D_{sd} \cdot r_p$
  注意，这里是指定一条链路 $e$ 去求该TE配置下会经过该链路的总流量，也即需要在所有SD对对应的转发路径集合 $P_{sd}$ 中寻找包含 $e$ 的路径 $p$ ，再对所有路径上经过的流量进行累加。
- MLU：由此得到网络的最大链路利用率如下。
  $\text{MLU} = \text{max}_{e \in E} \frac{f_e}{c(e)}$
  也即，对网络中的每一条链路 $e$ 都计算其 $f_e$ ，并除以该链路的容量，得到该链路的利用率，最后取所有链路利用率中的最大值，得到MLU。
- 在 $t$ 时刻，TE方案需要生成网络配置 $\mathcal{R}_t(D_1,\dots,D_{t-1})$ ，该配置是基于历史数据 $(D_1,\dots,D_{t-1})$ 得到的，我们的目标是生成一个TE配置方案，使得该方案较好地转发即将到来的 $D_t$ ，获得一个较低的MLU，目标函数如下：
  $\underset{\mathcal{R}_t(D_1, \dots, D_{t-1})}{\text{minimize}} \;\;\; M(\mathcal{R}(D_1,\dots,D_{t-1}),D_t) \tag{1}$
流量的不确定性

关键在于，我们必须同时考虑到可预测的流量和不可预测的突发流量。前者用流量需求矩阵 $D_t^{\text{expect}}$ 表示，可以使用某种流量预测技术从历史数据 $(D_1,\dots,D_{t-1})$ 推测出来。只考虑可预测的部分显然无法在突发流量场景下获取较好的网络性能，所以在计算TE配置时，需要考虑 $D_t^{\text{expect}}$ 和真实流量需求矩阵 $D_t$ 之间的差距。

FIGRET DESIGN

处理突发流量

定义一个集合来处理突发流量
- 原理
  
  假设一个集合 $\Delta$ ，其中的每个元素 $\delta$ 都表示一种特定的突发流量矩阵，这样就可以在考虑突发流量的情况下预测真实流量需求：
  $\hat{D}_t = \delta + D^\text{expect}$
  目标是找到一个TE配置，该配置应该能够给出最好的最坏情况下（针对 $\Delta$ 中所有的元素）性能保障，如下：
  $\underset{\mathcal{R}_t}{\text{minimize}} \;\;\; \text{max}_{\hat{D}_t \in \hat{\mathcal{D}}}M(\mathcal{R}_t, \hat{D}_t) \\ \text{s.t.} \;\;\; \hat{\mathcal{D}} = \{\hat{D}_t | \hat{D}_t = \delta + D^\text{expect}, \delta \in \Delta \} \tag{2}$
- 缺陷
  - 很难找到最合适的 $\Delta$ ，使得生成的TE配置能够在正常情况性能和突发情况性能之间产生最佳权衡。尽管可以使用切比雪夫不等式来量化 $\Delta$ ，使得概率 $P(D_t \notin \hat{\mathcal{D}})$ 不大于一个小值 $\alpha$ ，但 $D_t$ 仍可能不在 $\hat{\mathcal{D}}$ 之内，这时方程（2）就不再能够提供最坏性能保障。诚然，我们可以增加 $\Delta$ 集合中的元素，使得 $P(D_t \notin \hat{\mathcal{D}})$ 非常小，但这样可能会牺牲正常情况下的网络性能。
  - 如果 $\hat{\mathcal{D}}$ 集合非常大，计算代价也会比较高。
通过施加约束来处理突发流量
- 原理
  
  如果考虑突发流量矩阵 $\delta$ ，每条链路的利用率可以表示为： $\sum_{s,d \in V, p \in P_{sd}, e \in p}(D_{sd}^{\text{expect}} + \delta_{sd}) \cdot r_p / c(e)$ 。从这个式子可以看出，突发流量对链路的影响可以通过式子中的系数 $r_p / c(e)$ 进行约束，同时可以通过调整系数的上限来控制稳健性程度。
  
  上限如果比较高，流量配置方案就能给上限高的路径分配更大的 $r_p$ 。面对突发流量时，这可能导致这些路径在流量突增时出现过载，从而增加网络拥塞的风险。
  
  为了给不同路径设置不同水平的稳健性，需要利用不同SD对之间流量特征的不同，因此施加的约束（上限）函数如下：
  $\mathcal{F}:(s,d) \rightarrow \mathbb{R}^+$
  约束如下：
  $\forall s,d \in V, \forall p \in P_{sd}, \forall e \in p \;\;\; \frac{r_p}{c(e)} \leq \mathcal{F}((s,d)) \tag{3}$
  由于 $C_p = \text{min}_{e \in p} c(e)$ ，上式等价于：
  $\forall s,d \in V, \forall p \in P_{sd} \;\;\; \frac{r_p}{C_p} \leq \mathcal{F}((s,d)) \tag{4}$
  
  这个等价关系比较好证明，上推下、下推上都能得到。
  
  综上所述，确保比例系数 $\frac{r_p}{C_p}$ 低于某个限制，可以保证流量配置方案对于突发流量的稳健性。
  
  假设上限设定在一个值，那么系数最大只能与这个值相等，TE配置最多只能为该条路径分配对应的 $r_p$ 。若大部分情况下（正常/突发流量），该路径上的链路都能在一个比较健康的链路利用率下转发这个比例（ $r_p$ ）的流量，那么这条链路的工作稳定性就有了一定的保证。扩展到整个网络，如果上限设置得当，整个网络的稳健性也就得到了一定保障。
  
  因此，可以使用该系数表示TE配置的稳健性水平，定义路径敏感度如下：
  $\mathscr{S}_p = \frac{r_p}{C_p}$
  考虑路径敏感度，为目标函数加上约束：
  $\underset{\mathcal{R}_t}{\text{minimize}} \;\;\; M(\mathcal{R}_t, D_t^{\text{expect}}) \\ \text{s.t.} \;\;\; \mathscr{S}_p \leq \mathcal{F}((s,d)), \forall s, d \in V, \forall p \in P_{sd} \tag{5}$
  
  这里的约束不等式不止一个，数量由SD对的数量和每个SD对下转发路径的条数决定。
- $D_t^{\text{expect}}$ 和 $\mathcal{F}$ 的确定
  
  两者都是根据历史流量数据 $\{D_1,\dots,D_{t-1} \}$ 确定的，选择适合特定网络拓扑和流量模式的 $D_t^{\text{expect}}$ 和 $\mathcal{F}$ 是一个复杂的过程。
  - 传统方法假设真实的数据流能够完全被预测的流量需求矩阵 $D_t^{\text{expect}}$ 所表示，且不对 $\mathcal{F}$ 做限制（即 $\mathcal{F}((s,d)) \equiv +\infty$ ），在预测后直接优化MLU。
  - 去敏感化方法将函数 $\mathcal{F}$ 设置为一个常数，对所有SD对都相同，这种方法无法在提高抗突发能力和优化平均性能之间实现平衡。
  - 还有的方法将路径敏感度 $\mathscr{S}_p$ 作为目标，试图最小化所有路径敏感度中的最大值，这种方法同样没有考虑到不同SD对之间的流量模式差异。

计算TE方案

two-stage method
- 原理
  
  首先显式地估算出 $D_t^{\text{expect}}$ 和 $\mathcal{F}$ ，然后使用线性规划算法来求解方程（5）。
- 问题
  - 某些SD对之间的突发流量情况比较频繁，难以预测出一个合适的 $D_t^{\text{expect}}$ 。
  - 上游任务（估算 $D_t^{\text{expect}}$ 和 $\mathcal{F}$ ）和下游任务（优化MLU）之间不匹配。
    
    估算 $D_t^{\text{expect}}$ 通常使用均方误差，而均方误差的计算与网络拓扑结构无关（这可能导致计算出来的TE配置中，某些链路可能会被过度使用或不足使用，进而引发网络拥堵或资源浪费），网络拓扑结构又是MLU优化中的重要因素，因此说上下游任务之间适配不佳。
    
    比如，某些SD对之间存在高容量路径（这就与网络拓扑结构有关）的情况下，精确预测出流量需求矩阵就变得没那么有必要了。
    
    类似地，估算 $\mathcal{F}$ 也应该在考虑流量特征的同时考虑网络拓扑结构。
  - 线性规划可能引入较高的计算复杂度，无法扩展至大型网络结构。
end-to-end method
- 原理
  
  不显式地预测 $D_t^{\text{expect}}$ 和 $\mathcal{F}$ ，而是直接在历史数据 $\{D_1,\dots,D_{t-1} \}$ 和TE配置 $\mathcal{R}_t$ 之间建立联系，目的是优化MLU并确保网络的稳健性。
- 优点
  
  能够考虑网络拓扑的影响，避免了上游流量预测任务和下游网络优化任务之间的不匹配。
- 实施
  
  由于不显式地预测 $D_t^{\text{expect}}$ 和 $\mathcal{F}$ ，该方案无法清晰地建立一个如方程5的优化问题，所以不能使用线性规划求解。文章设计了一个具备突发感知能力的损失函数，采用深度神经网络求解出TE配置。

损失函数设计

为了保证深度神经网络输入的一致性，训练时，FIGRET只接收窗口值 $H$ 大小的历史数据 $\{D_{t-H},\dots,D_{t-1}\}$ ，这样也避免了 $t$ 较大时需要处理的流量数据过多的问题。然后，FIGRET输出一个TE配置 $R_t$ ，两者之间关系如下：

R_t = \pi_\theta(D_{t-H,\dots,D_{t-1}})

通过对方程5做拉格朗日松弛，得到：

\underset{\mathcal{R}_t,\lambda}{\text{minimize}} \;\;\; L(\mathcal{R}_t, \lambda) = M(\mathcal{R}_t, D_t^{\text{expect}}) \\ + \sum_{s,d \in V} \sum_{p \in P_{sd}} \lambda_{sd,p} (\mathscr{S}_p - \mathcal{F}((s,d))) \\ \text{s.t.} \;\;\; \lambda_{sd,p} \geq 0, \forall s, d \in V, \forall p \in P_{sd} \tag{6}

Loss for MLU

损失函数的第一部分负责优化MLU：
$\mathcal{L}_1 = M(R_t,D_t) \tag{7}$
FIGRET在训练完成后，通过第一个损失函数隐式地学习到了一个概率分布 $$ P(D^{\text{expect}}t | D{t-1}, \ldots, D_{t-H}) $$。这个分布表示给定过去的流量数据时，不同的流量需求矩阵 $$ D^{\text{expect}}_t $$ 发生的可能性。

这里需要弄清楚概率分布的形式，比如说在 $t$ 时刻，历史流量数据如下：
$D_{t-1} = \begin{bmatrix} 10 & 20 \\ 15 & 25 \end{bmatrix}, \quad D_{t-2} = \begin{bmatrix} 12 & 18 \\ 14 & 24 \end{bmatrix}, \quad D_{t-3} = \begin{bmatrix} 9 & 22 \\ 16 & 23 \end{bmatrix}$
通过训练，FIGRET可以学习到条件概率分布，比如：
$P(D^{\text{expect}}_t = \begin{bmatrix} 11 & 20 \\ 17 & 24 \end{bmatrix}) = 0.4 \\ P(D^{\text{expect}}_t = \begin{bmatrix} 12 & 22 \\ 16 & 23 \end{bmatrix}) = 0.3 \\ P(D^{\text{expect}}_t = \begin{bmatrix} 10 & 19 \\ 15 & 26 \end{bmatrix}) = 0.2 \\ P(D^{\text{expect}}_t = \begin{bmatrix} 13 & 21 \\ 18 & 25 \end{bmatrix}) = 0.1$

然后，FIGRET输出一个流量配置 $$ R_t $$，该配置能够优化数学期望 $\mathbb{E}_{D^{\text{expect}}_t}[M(R_t,D^{\text{expect}}_t)]$ 。

即FIGRET首先学习到了一个关于流量需求矩阵的概率分布，而后给出一个流量配置，这个配置能够在该概率分布下得到一个较优的数学期望。

数学期望的内容是损失函数的第一部分（优化MLU），结合上面给出的概率分布例子理解，该数学期望求得不同流量需求矩阵下MLU的平均值。

在训练初期，模型可能随机给出一个流量配置，在该配置下求数学期望得到的值可能较大。随着训练进程推进，模型给出的流量配置越来越适合于这些可能的流量需求矩阵，能够在对应的需求（不是显式测出一个，而是多个矩阵的概率分布）下高效地转发流量。

综上所述，FIGRET最终输出的流量配置能够优化这个数学期望。
Loss for fine-grained robustness

损失函数的第二部分旨在反映路径敏感度所施加的约束，由于文章采用的端到端方法没有显式地计算 $\mathcal{F}$ ，所以不能如方程6直接在损失函数中使用 $\sum_{s,d \in V} \sum_{p \in P_{sd}} \lambda_{sd,p} (\mathscr{S}_p - \mathcal{F}((s,d)))$ ，因此文章设计了一种启发式方案来构建损失函数的第二部分。

假设在训练期（1~T），从源节点 $s$ 到目标节点 $d$ 的流量需求 $D_{sd}$ 的方差用 $\sigma ^2 _{D_{sd},[1-T]}$ 表示。配置 $R_t$ 下，记 $\mathscr{S}_{sd}^{\text{max}}$ 为在所有为该SD对服务的路径中最大的路径敏感度。由此得到损失函数的第二部分：
$\mathcal{L}_2 = \underset{\forall s,d \in V}{\sum} \; \sigma^2 _{D_{sd},[1-T]} \times \mathscr{S}_{sd}^{\text{max}} \tag{8}$
将SD对分为两类：稳定流量模式 $ (s, d){\text{stable}} $ 和突发流量模式 $ (s, d){\text{bursty}} $。对于稳定流量模式，约束值 $ F((s, d){\text{stable}}) $ 较高（即不做过多约束）；而对于突发流量模式，约束值 $ F((s, d){\text{bursty}}) $ 较低（约束更严格）。

从原始项 $\sum_{s,d \in V} \sum_{p \in P_{sd}} \lambda_{sd,p} (\mathscr{S}_p - \mathcal{F}((s,d)))$ 中看，如果配置为突发流量模式的SD对设置了较高的 $r_p$ ，那么其 $\mathscr{S}_p$ 也会相应变大，进而导致 $(\mathscr{S}_p - \mathcal{F}((s,d)))$ 变大，不利于损失函数的最小化。

应对突发流量时，应该为每条路径分配较小的流量比例，防止链路过载。

公式8实现了类似的功能，对于每个源-目的对（SD pair）计算流量需求的方差 $\sigma^2_{D_{sd},[1-T]}$ ，这个方差反映了流量在时间 1 到 T 之间的变化程度。接下来，使用服务于相应 SD 对的路径的最大路径灵敏度 $\mathscr{S}^{\text{max}}_{sd}$ 来加权这些方差。

对于稳定SD对， $\sigma^2_{D_{sd},[1-T]}$ 比较小，因此将 $\mathscr{S}^{\text{max}}_{sd}$ 放大仍能够保持其乘积较小。

对于不稳定SD对， $\sigma^2_{D_{sd},[1-T]}$ 比较大，因此将 $\mathscr{S}^{\text{max}}_{sd}$ 放大不利于损失函数的最小化。

因此，模型通过训练，会自发为稳定和不稳定的SD对对应的转发路径设置不同的 $r_p$ 来适应普通流量/突发流量的转发，以最小化损失函数。

通过同时考虑损失项 $L_1$ 和 $L_2$ ，模型能够在保持MLU优化的同时调整不同SD对的路径敏感度约束。这种方法确保网络不仅实现了 MLU 优化目标，还以细粒度的方式增强了不同SD对适应突发流量的能力。

Papers:FIGRET